Skip to content

Latest commit

 

History

History
860 lines (795 loc) · 56.3 KB

3.深度学习.md

File metadata and controls

860 lines (795 loc) · 56.3 KB

3.1 计算AlexNet、VGG19、ResNet152三个网络中的神经元数目及可训练的参数数目。

3.1.1 AlexNet

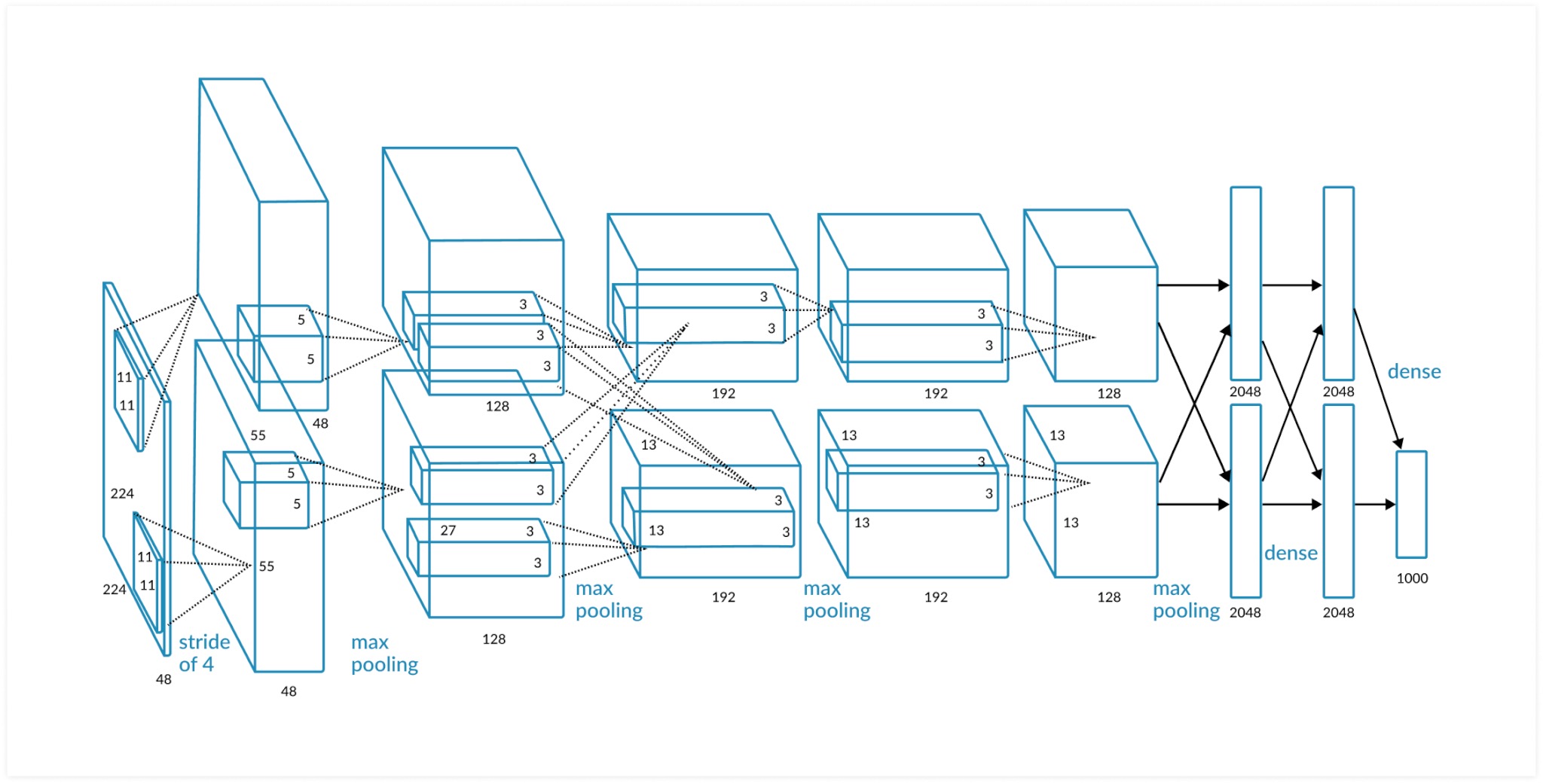
AlexNet Banner

AlexNet的论文里为了方便使用两块GPU一起训练，网络分了两路，合并成一路网络来看，共有五层卷积层，三层全联接层，但是在分析神经元个数及可训练参数的时候需要注意，使用两块GPU进行训练的网络，有部分卷积和前一级的两个特征图相连，而有部分卷积只和前一级的单块GPU上的特征图相连，具体的链接关系可以参考上图。

这里首先需要明确一下神经元的定义，题目中要计算的神经元的个数，那对于卷积运算神经元的数目应该如何计算？

一个神经元表示的是w*x+b​的过程，而对于卷积运算来说，feature map取代了全连接层的layer、所以feature map的大小就是神经元的个数。但是对于特征图经过池化层之后得到的下一次卷积的输入，及池化后的结果不把其计算到神经元数目之中，其运算的本质是比大小，不明显符合神经元的特征。

Convolution Layer Kernel Size Channel Number Output Size
conv_1 11*11 96 (27,27,96)
conv_2 5*5 256 (13,13,256)
conv_3 3*3 384 (13,13,384)
conv_4 3*3 384 (13,13,384)
conv_5 3*3 256 (6,6,256)

因为部分卷积层之后涉及到池化，所以不单独在表格后面列出神经元的数目的计算程式。

第一层是输入层、神经元的数目： $$ 2272273 = 154587 $$ 无可训练参数。

对第一层卷积，因为Output Size的大小实际上是经过Max Pooling过的，所以神经元数目： $$ 555596=290400 $$ 可训练参数： $$ weights+bias = 9611113+96 = 34944 $$ 对第二层卷积，依然有Max Pooling神经元数目： $$ 2727256=186624 $$ 可训练参数： $$ weights+bias = 2(128485*5+128)=307456 $$

对于第三层卷积，没有Max Pooling神经元数目： $$ 1313384 = 64896 $$ 可训练参数，这里是与前面的两个特征图都连接的： $$ weights+bias = 38433*256+384=885120 $$ 对于第四层卷积，神经元数目：

$$ 1313384=64896 $$ 可训练参数: $$ weights+bias = 2*(19233192+192)=663936 $$ 对于第五层卷积，神经元数目： $$ 1313256 = 43264 $$ 可训练参数: $$ weights+bias=2(1281923*3+128)=442624 $$

Fully-Connect Layer Nodes 神经元数目 可训练参数
FC1 4096 4096 $409666*256+4096=37752832$
FC2 4096 4096 $4096*4096+4096=16781312$
FC3 1000 1000 $4096*1000+1000=4087000$

总神经元数目： $$ 154587+290400+186624+64896+64896+43264+4096+4096+1000=813859 $$ 可训练参数 $$ 34944+307456+885120+663936+442624+37752832+16781312+4087000=60955224 $$ 有关于卷积运算和全联接层的神经元参数计算和可训练参数的计算方法已经在[3.1.1](#3.1.1 AlexNet)里说的很详细了，对于接下来要分析的VGG19、以及多达一百多层的ResNet158，把一层一层的神经元个数与可训练参数都罗列出来显然是不合适的，我使用Pytorch来分析可训练参数以参数数目。

借鉴了方案来自：https://github.com/TylerYep/torchinfo

程式代码：https://github.com/LeiWang1999/AICS-Course/tree/master/Code/3.1.netcalculation.pytorch

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
├─Sequential: 1-1                        [1, 256, 6, 6]            --
|    └─Conv2d: 2-1                       [1, 64, 55, 55]           23,296
|    └─ReLU: 2-2                         [1, 64, 55, 55]           --
|    └─MaxPool2d: 2-3                    [1, 64, 27, 27]           --
|    └─Conv2d: 2-4                       [1, 192, 27, 27]          307,392
|    └─ReLU: 2-5                         [1, 192, 27, 27]          --
|    └─MaxPool2d: 2-6                    [1, 192, 13, 13]          --
|    └─Conv2d: 2-7                       [1, 384, 13, 13]          663,936
|    └─ReLU: 2-8                         [1, 384, 13, 13]          --
|    └─Conv2d: 2-9                       [1, 256, 13, 13]          884,992
|    └─ReLU: 2-10                        [1, 256, 13, 13]          --
|    └─Conv2d: 2-11                      [1, 256, 13, 13]          590,080
|    └─ReLU: 2-12                        [1, 256, 13, 13]          --
|    └─MaxPool2d: 2-13                   [1, 256, 6, 6]            --
├─AdaptiveAvgPool2d: 1-2                 [1, 256, 6, 6]            --
├─Sequential: 1-3                        [1, 1000]                 --
|    └─Dropout: 2-14                     [1, 9216]                 --
|    └─Linear: 2-15                      [1, 4096]                 37,752,832
|    └─ReLU: 2-16                        [1, 4096]                 --
|    └─Dropout: 2-17                     [1, 4096]                 --
|    └─Linear: 2-18                      [1, 4096]                 16,781,312
|    └─ReLU: 2-19                        [1, 4096]                 --
|    └─Linear: 2-20                      [1, 1000]                 4,097,000
==========================================================================================
Total params: 61,100,840
Trainable params: 61,100,840
Non-trainable params: 0
Total mult-adds (M): 775.28
==========================================================================================
Input size (MB): 0.57
Forward/backward pass size (MB): 3.77
Params size (MB): 233.08
Estimated Total Size (MB): 237.43
==========================================================================================

3.1.2 VGG19

VGG

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
├─Sequential: 1-1                        [1, 512, 7, 7]            --
|    └─Conv2d: 2-1                       [1, 64, 224, 224]         1,792
|    └─ReLU: 2-2                         [1, 64, 224, 224]         --
|    └─Conv2d: 2-3                       [1, 64, 224, 224]         36,928
|    └─ReLU: 2-4                         [1, 64, 224, 224]         --
|    └─MaxPool2d: 2-5                    [1, 64, 112, 112]         --
|    └─Conv2d: 2-6                       [1, 128, 112, 112]        73,856
|    └─ReLU: 2-7                         [1, 128, 112, 112]        --
|    └─Conv2d: 2-8                       [1, 128, 112, 112]        147,584
|    └─ReLU: 2-9                         [1, 128, 112, 112]        --
|    └─MaxPool2d: 2-10                   [1, 128, 56, 56]          --
|    └─Conv2d: 2-11                      [1, 256, 56, 56]          295,168
|    └─ReLU: 2-12                        [1, 256, 56, 56]          --
|    └─Conv2d: 2-13                      [1, 256, 56, 56]          590,080
|    └─ReLU: 2-14                        [1, 256, 56, 56]          --
|    └─Conv2d: 2-15                      [1, 256, 56, 56]          590,080
|    └─ReLU: 2-16                        [1, 256, 56, 56]          --
|    └─Conv2d: 2-17                      [1, 256, 56, 56]          590,080
|    └─ReLU: 2-18                        [1, 256, 56, 56]          --
|    └─MaxPool2d: 2-19                   [1, 256, 28, 28]          --
|    └─Conv2d: 2-20                      [1, 512, 28, 28]          1,180,160
|    └─ReLU: 2-21                        [1, 512, 28, 28]          --
|    └─Conv2d: 2-22                      [1, 512, 28, 28]          2,359,808
|    └─ReLU: 2-23                        [1, 512, 28, 28]          --
|    └─Conv2d: 2-24                      [1, 512, 28, 28]          2,359,808
|    └─ReLU: 2-25                        [1, 512, 28, 28]          --
|    └─Conv2d: 2-26                      [1, 512, 28, 28]          2,359,808
|    └─ReLU: 2-27                        [1, 512, 28, 28]          --
|    └─MaxPool2d: 2-28                   [1, 512, 14, 14]          --
|    └─Conv2d: 2-29                      [1, 512, 14, 14]          2,359,808
|    └─ReLU: 2-30                        [1, 512, 14, 14]          --
|    └─Conv2d: 2-31                      [1, 512, 14, 14]          2,359,808
|    └─ReLU: 2-32                        [1, 512, 14, 14]          --
|    └─Conv2d: 2-33                      [1, 512, 14, 14]          2,359,808
|    └─ReLU: 2-34                        [1, 512, 14, 14]          --
|    └─Conv2d: 2-35                      [1, 512, 14, 14]          2,359,808
|    └─ReLU: 2-36                        [1, 512, 14, 14]          --
|    └─MaxPool2d: 2-37                   [1, 512, 7, 7]            --
├─AdaptiveAvgPool2d: 1-2                 [1, 512, 7, 7]            --
├─Sequential: 1-3                        [1, 1000]                 --
|    └─Linear: 2-38                      [1, 4096]                 102,764,544
|    └─ReLU: 2-39                        [1, 4096]                 --
|    └─Dropout: 2-40                     [1, 4096]                 --
|    └─Linear: 2-41                      [1, 4096]                 16,781,312
|    └─ReLU: 2-42                        [1, 4096]                 --
|    └─Dropout: 2-43                     [1, 4096]                 --
|    └─Linear: 2-44                      [1, 1000]                 4,097,000
==========================================================================================
Total params: 143,667,240
Trainable params: 143,667,240
Non-trainable params: 0
Total mult-adds (G): 19.78
==========================================================================================
Input size (MB): 0.57
Forward/backward pass size (MB): 113.38
Params size (MB): 548.05
Estimated Total Size (MB): 662.00
==========================================================================================

3.1.3 ResNet152

Estimated Total Size (MB): 662.00
==========================================================================================
==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
├─Conv2d: 1-1                            [1, 64, 112, 112]         9,408
├─BatchNorm2d: 1-2                       [1, 64, 112, 112]         128
├─ReLU: 1-3                              [1, 64, 112, 112]         --
├─MaxPool2d: 1-4                         [1, 64, 56, 56]           --
├─Sequential: 1-5                        [1, 256, 56, 56]          --
|    └─Bottleneck: 2-1                   [1, 256, 56, 56]          --
|    |    └─Conv2d: 3-1                  [1, 64, 56, 56]           4,096
|    |    └─BatchNorm2d: 3-2             [1, 64, 56, 56]           128
|    |    └─ReLU: 3-3                    [1, 64, 56, 56]           --
|    |    └─Conv2d: 3-4                  [1, 64, 56, 56]           36,864
|    |    └─BatchNorm2d: 3-5             [1, 64, 56, 56]           128
|    |    └─ReLU: 3-6                    [1, 64, 56, 56]           --
|    |    └─Conv2d: 3-7                  [1, 256, 56, 56]          16,384
|    |    └─BatchNorm2d: 3-8             [1, 256, 56, 56]          512
|    |    └─Sequential: 3-9              [1, 256, 56, 56]          16,896
|    |    └─ReLU: 3-10                   [1, 256, 56, 56]          --
|    └─Bottleneck: 2-2                   [1, 256, 56, 56]          --
|    |    └─Conv2d: 3-11                 [1, 64, 56, 56]           16,384
|    |    └─BatchNorm2d: 3-12            [1, 64, 56, 56]           128
|    |    └─ReLU: 3-13                   [1, 64, 56, 56]           --
|    |    └─Conv2d: 3-14                 [1, 64, 56, 56]           36,864
|    |    └─BatchNorm2d: 3-15            [1, 64, 56, 56]           128
|    |    └─ReLU: 3-16                   [1, 64, 56, 56]           --
|    |    └─Conv2d: 3-17                 [1, 256, 56, 56]          16,384
|    |    └─BatchNorm2d: 3-18            [1, 256, 56, 56]          512
|    |    └─ReLU: 3-19                   [1, 256, 56, 56]          --
|    └─Bottleneck: 2-3                   [1, 256, 56, 56]          --
|    |    └─Conv2d: 3-20                 [1, 64, 56, 56]           16,384
|    |    └─BatchNorm2d: 3-21            [1, 64, 56, 56]           128
|    |    └─ReLU: 3-22                   [1, 64, 56, 56]           --
|    |    └─Conv2d: 3-23                 [1, 64, 56, 56]           36,864
|    |    └─BatchNorm2d: 3-24            [1, 64, 56, 56]           128
|    |    └─ReLU: 3-25                   [1, 64, 56, 56]           --
|    |    └─Conv2d: 3-26                 [1, 256, 56, 56]          16,384
|    |    └─BatchNorm2d: 3-27            [1, 256, 56, 56]          512
|    |    └─ReLU: 3-28                   [1, 256, 56, 56]          --
├─Sequential: 1-6                        [1, 512, 28, 28]          --
|    └─Bottleneck: 2-4                   [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-29                 [1, 128, 56, 56]          32,768
|    |    └─BatchNorm2d: 3-30            [1, 128, 56, 56]          256
|    |    └─ReLU: 3-31                   [1, 128, 56, 56]          --
|    |    └─Conv2d: 3-32                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-33            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-34                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-35                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-36            [1, 512, 28, 28]          1,024
|    |    └─Sequential: 3-37             [1, 512, 28, 28]          132,096
|    |    └─ReLU: 3-38                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-5                   [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-39                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-40            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-41                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-42                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-43            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-44                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-45                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-46            [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-47                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-6                   [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-48                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-49            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-50                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-51                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-52            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-53                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-54                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-55            [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-56                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-7                   [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-57                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-58            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-59                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-60                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-61            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-62                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-63                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-64            [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-65                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-8                   [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-66                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-67            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-68                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-69                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-70            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-71                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-72                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-73            [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-74                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-9                   [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-75                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-76            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-77                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-78                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-79            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-80                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-81                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-82            [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-83                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-10                  [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-84                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-85            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-86                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-87                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-88            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-89                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-90                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-91            [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-92                   [1, 512, 28, 28]          --
|    └─Bottleneck: 2-11                  [1, 512, 28, 28]          --
|    |    └─Conv2d: 3-93                 [1, 128, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-94            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-95                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-96                 [1, 128, 28, 28]          147,456
|    |    └─BatchNorm2d: 3-97            [1, 128, 28, 28]          256
|    |    └─ReLU: 3-98                   [1, 128, 28, 28]          --
|    |    └─Conv2d: 3-99                 [1, 512, 28, 28]          65,536
|    |    └─BatchNorm2d: 3-100           [1, 512, 28, 28]          1,024
|    |    └─ReLU: 3-101                  [1, 512, 28, 28]          --
├─Sequential: 1-7                        [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-12                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-102                [1, 256, 28, 28]          131,072
|    |    └─BatchNorm2d: 3-103           [1, 256, 28, 28]          512
|    |    └─ReLU: 3-104                  [1, 256, 28, 28]          --
|    |    └─Conv2d: 3-105                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-106           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-107                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-108                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-109           [1, 1024, 14, 14]         2,048
|    |    └─Sequential: 3-110            [1, 1024, 14, 14]         526,336
|    |    └─ReLU: 3-111                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-13                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-112                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-113           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-114                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-115                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-116           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-117                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-118                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-119           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-120                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-14                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-121                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-122           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-123                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-124                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-125           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-126                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-127                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-128           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-129                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-15                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-130                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-131           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-132                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-133                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-134           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-135                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-136                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-137           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-138                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-16                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-139                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-140           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-141                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-142                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-143           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-144                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-145                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-146           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-147                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-17                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-148                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-149           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-150                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-151                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-152           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-153                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-154                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-155           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-156                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-18                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-157                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-158           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-159                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-160                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-161           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-162                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-163                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-164           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-165                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-19                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-166                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-167           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-168                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-169                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-170           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-171                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-172                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-173           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-174                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-20                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-175                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-176           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-177                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-178                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-179           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-180                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-181                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-182           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-183                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-21                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-184                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-185           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-186                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-187                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-188           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-189                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-190                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-191           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-192                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-22                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-193                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-194           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-195                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-196                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-197           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-198                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-199                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-200           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-201                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-23                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-202                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-203           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-204                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-205                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-206           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-207                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-208                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-209           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-210                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-24                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-211                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-212           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-213                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-214                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-215           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-216                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-217                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-218           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-219                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-25                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-220                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-221           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-222                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-223                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-224           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-225                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-226                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-227           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-228                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-26                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-229                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-230           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-231                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-232                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-233           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-234                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-235                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-236           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-237                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-27                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-238                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-239           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-240                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-241                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-242           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-243                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-244                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-245           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-246                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-28                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-247                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-248           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-249                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-250                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-251           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-252                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-253                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-254           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-255                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-29                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-256                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-257           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-258                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-259                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-260           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-261                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-262                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-263           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-264                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-30                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-265                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-266           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-267                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-268                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-269           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-270                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-271                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-272           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-273                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-31                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-274                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-275           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-276                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-277                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-278           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-279                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-280                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-281           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-282                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-32                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-283                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-284           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-285                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-286                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-287           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-288                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-289                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-290           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-291                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-33                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-292                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-293           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-294                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-295                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-296           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-297                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-298                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-299           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-300                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-34                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-301                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-302           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-303                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-304                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-305           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-306                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-307                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-308           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-309                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-35                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-310                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-311           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-312                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-313                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-314           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-315                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-316                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-317           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-318                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-36                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-319                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-320           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-321                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-322                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-323           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-324                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-325                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-326           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-327                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-37                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-328                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-329           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-330                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-331                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-332           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-333                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-334                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-335           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-336                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-38                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-337                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-338           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-339                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-340                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-341           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-342                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-343                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-344           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-345                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-39                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-346                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-347           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-348                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-349                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-350           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-351                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-352                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-353           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-354                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-40                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-355                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-356           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-357                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-358                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-359           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-360                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-361                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-362           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-363                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-41                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-364                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-365           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-366                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-367                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-368           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-369                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-370                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-371           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-372                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-42                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-373                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-374           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-375                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-376                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-377           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-378                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-379                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-380           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-381                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-43                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-382                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-383           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-384                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-385                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-386           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-387                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-388                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-389           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-390                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-44                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-391                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-392           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-393                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-394                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-395           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-396                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-397                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-398           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-399                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-45                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-400                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-401           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-402                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-403                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-404           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-405                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-406                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-407           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-408                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-46                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-409                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-410           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-411                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-412                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-413           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-414                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-415                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-416           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-417                  [1, 1024, 14, 14]         --
|    └─Bottleneck: 2-47                  [1, 1024, 14, 14]         --
|    |    └─Conv2d: 3-418                [1, 256, 14, 14]          262,144
|    |    └─BatchNorm2d: 3-419           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-420                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-421                [1, 256, 14, 14]          589,824
|    |    └─BatchNorm2d: 3-422           [1, 256, 14, 14]          512
|    |    └─ReLU: 3-423                  [1, 256, 14, 14]          --
|    |    └─Conv2d: 3-424                [1, 1024, 14, 14]         262,144
|    |    └─BatchNorm2d: 3-425           [1, 1024, 14, 14]         2,048
|    |    └─ReLU: 3-426                  [1, 1024, 14, 14]         --
├─Sequential: 1-8                        [1, 2048, 7, 7]           --
|    └─Bottleneck: 2-48                  [1, 2048, 7, 7]           --
|    |    └─Conv2d: 3-427                [1, 512, 14, 14]          524,288
|    |    └─BatchNorm2d: 3-428           [1, 512, 14, 14]          1,024
|    |    └─ReLU: 3-429                  [1, 512, 14, 14]          --
|    |    └─Conv2d: 3-430                [1, 512, 7, 7]            2,359,296
|    |    └─BatchNorm2d: 3-431           [1, 512, 7, 7]            1,024
|    |    └─ReLU: 3-432                  [1, 512, 7, 7]            --
|    |    └─Conv2d: 3-433                [1, 2048, 7, 7]           1,048,576
|    |    └─BatchNorm2d: 3-434           [1, 2048, 7, 7]           4,096
|    |    └─Sequential: 3-435            [1, 2048, 7, 7]           2,101,248
|    |    └─ReLU: 3-436                  [1, 2048, 7, 7]           --
|    └─Bottleneck: 2-49                  [1, 2048, 7, 7]           --
|    |    └─Conv2d: 3-437                [1, 512, 7, 7]            1,048,576
|    |    └─BatchNorm2d: 3-438           [1, 512, 7, 7]            1,024
|    |    └─ReLU: 3-439                  [1, 512, 7, 7]            --
|    |    └─Conv2d: 3-440                [1, 512, 7, 7]            2,359,296
|    |    └─BatchNorm2d: 3-441           [1, 512, 7, 7]            1,024
|    |    └─ReLU: 3-442                  [1, 512, 7, 7]            --
|    |    └─Conv2d: 3-443                [1, 2048, 7, 7]           1,048,576
|    |    └─BatchNorm2d: 3-444           [1, 2048, 7, 7]           4,096
|    |    └─ReLU: 3-445                  [1, 2048, 7, 7]           --
|    └─Bottleneck: 2-50                  [1, 2048, 7, 7]           --
|    |    └─Conv2d: 3-446                [1, 512, 7, 7]            1,048,576
|    |    └─BatchNorm2d: 3-447           [1, 512, 7, 7]            1,024
|    |    └─ReLU: 3-448                  [1, 512, 7, 7]            --
|    |    └─Conv2d: 3-449                [1, 512, 7, 7]            2,359,296
|    |    └─BatchNorm2d: 3-450           [1, 512, 7, 7]            1,024
|    |    └─ReLU: 3-451                  [1, 512, 7, 7]            --
|    |    └─Conv2d: 3-452                [1, 2048, 7, 7]           1,048,576
|    |    └─BatchNorm2d: 3-453           [1, 2048, 7, 7]           4,096
|    |    └─ReLU: 3-454                  [1, 2048, 7, 7]           --
├─AdaptiveAvgPool2d: 1-9                 [1, 2048, 1, 1]           --
├─Linear: 1-10                           [1, 1000]                 2,049,000
==========================================================================================
Total params: 60,192,808
Trainable params: 60,192,808
Non-trainable params: 0
Total mult-adds (G): 11.63
==========================================================================================
Input size (MB): 0.57
Forward/backward pass size (MB): 344.16
Params size (MB): 229.62
Estimated Total Size (MB): 574.35
==========================================================================================

3.2 计算习题3.1中三个网络完成一次正向过程所需要的乘法数量和加法数量。

在[3.1](#3.1 计算AlexNet、VGG19、ResNet152三个网络中的神经元数目及可训练的参数数目)中，使用torchinfo计算出了所有的乘加法数量，即macs操作数。

不明白题目的意思是不是需要把乘法数量和加法数量分开来计算，如果自己计算的话，碰到指数函数怎么算乘法和加法的数量呢？

3.3 简述错误率与IoU、mAP的关系

这部分不止可以参考书上，另外附上一个我很喜欢的up讲解的视频链接：https://www.bilibili.com/video/BV1ez4y1X7g2

测试结果 实际情况
正例(Positive) 反例(Negative)
正例(Positive) 真正例(True Positive, TP) 假正例(False Positive, FP)
反例(Negative) 假反例(False Negative, FN) 真反例(True Negative, TN)

3.4 简述训练过程中收敛、训练精度和测试精度之间的关系。

训练过程中的收敛，指的是损失函数的收敛。

每经过一次正向传播都会得到一段输出，将它与目标输出计算之后得出Loss，并且可以在训练集上得到训练精度，验证集上得到验证精度。测试精度是我们最终在未知的图片上的到的精度。

模型如果收敛了，那么训练精度就会提高，但验证精度不一定会提高。我们可以通过观察验证精度，保存在验证精度最好的模型，也可以使用early stopping技术来提前终止掉训练过程。

一般来讲，训练精度>验证精度>测试精度

3.5 试给出SVM和AlexNet在解决ImageNet图像分类问题的过程中对计算量的需求，并简述原因。

贴一个李宏毅的SVM讲解视频：https://www.bilibili.com/video/BV14W411u78t?t=3582

一般而言对于计算量，我们对于深度神经网络关注他的加法和乘法(MACs)数量，因为加法和乘法是其主要的运算，而对于SVM这类传统的机器学习方法，我们一般关注的是算法复杂度。

如果仅看推理过程，则对于小样本的分类问题，SVM和AlexNet的算法复杂度都可以看做是O(n)，但是对于复杂样本，SVM的算法复杂度会接近O(n*n)，而AlexNet的复杂度还保持在O(n)。

3.6 简述R-CNN、Fast R-CNN和Faster R-CNN的区别。

推荐一个我喜欢的UP的视频：https://www.bilibili.com/video/BV1af4y1m7iL

R-CNN的算法流程可以分为4个步骤：

  • 一张图像生成1K～2K个候选区域（使用 Selective Search方法）
  • 对每个候选区域，使用深度网络提取特征
  • 特征送入每一类SVM分类器，判断是否属于该类
  • 使用回归器精细修正候选框位置

Fast R-CNN算法流程可以分为3个步骤：

  • 一张图像生成1K～2K个候选区域（使用 Selective Search方法）
  • 将图像输入网络得到相应的特征图，将SS算法生成的候选框投影到特征图上获得相应的特征矩阵
  • 将每个特征矩阵通过ROI pooling层缩放阿斗7x7大小的特征图，接着将特征图展平成一系列全联接层得到预测结果

Faster R-CNN算法流程可以分为3个步骤：

  • 将图像输入网络得到相应的特征图
  • 使用RPN结构生成候选框，将RPN生成的候选框投影到特征图上获得相应的特征矩阵
  • 将每个特征矩阵通过ROI pooling层缩放阿斗7x7大小的特征图，接着将特征图展平成一系列全联接层得到预测结果

3.7 简述LSTM标准模型中三个门的主要作用，并给出计算公式。

  1. 遗忘门单元用来控制需要记住前一时刻单元状态的多少内容，并通过sigmoid函数将遗忘门的值限制在0到1之间。第t时刻的遗忘门单元为：

$$ f^{(t)} = \delta(U^f x^{(t)}+W^f h^{(t-1)}+b^f) $$

  1. 输入门单元用来控制写入多少输入信息到当前状态。其计算方法与遗忘门蕾丝，也是通过sigmoid函数将取值范围限制在0到1之间。第t时刻的输入门单元为：

$$ i^{(t)}=f^{(t)} = \delta(U^i x^{(t)}+W^i h^{(t-1)}+b^i) $$

  1. 输出门单元可以控制当前单元状态的输出。第t时刻的输出门单元为：

$$ g^{(t)}=\delta(U^o x^{(t)}+W^o h^{(t-1)}+b^o) $$

（摘录自课本 Page 88-89）

3.8 简述GAN的训练过程。

生成对抗网络(Generative Adversarial Net, GAN)分为两个部分，生成网络(NN Generator)和判别网络(Discriminator)。

在训练阶段，我们需要对生成网路和判别网络分别进行迭代训练，首先从数据集里sample出一小部分训练数据，然后fix住生成网络的参数，训练判别网络，使其对训练数据的输出越大越好、对生成网络生成的杂讯输出越小越好。接着fix住判别网络的参数，训练生成网络，让生成网络的输出经过判别网络之后的值越大越好，然后不断迭代训练。

3.9 简述图像风格迁移应用的基本过程。

首先输入内容图像p和风格图像a，图像风格迁移需要把二者的特征图结合起来。将内容图像和特征图像分别经过CNN生成各自的特征图，组成内容特征集P和风格特征集A。然后输入一张随机噪声图像x，x通过CNN生成的特征图构成内容特征集F和风格特征集G，然后由P、A、F、G计算目标损失函数。通过优化损失函数来调整图像x，使得内容特征集F与P接近、风格特征集G与A接近，经过多轮反复调整，可以使得中间图像在内容上与内容图像一致，在风格上与风格图像一致。（摘录自课本 Page 96）

3.10 试在MNIST数据集上训练一个多层感知机网络，网络规模拓扑可自定义，要求模型精度达到95%以上。

在本题，我使用了深度学习框架Caffe作为平台，搭建的多层感知机的prototxt文件和solver点击下方的链接访问：

https://github.com/LeiWang1999/AICS-Course/tree/master/Code/3.11.minist.fc.caffe

训练的精度达到97.9%，log如下：

I0119 09:06:08.694823   332 data_layer.cpp:73] Restarting data prefetching from start.
I0119 09:06:08.695462   327 solver.cpp:397]     Test net output #0: accuracy = 0.9792
I0119 09:06:08.695490   327 solver.cpp:397]     Test net output #1: loss = 0.0686949 (* 1 = 0.0686949 loss)
I0119 09:06:08.695518   327 solver.cpp:315] Optimization Done.
I0119 09:06:08.695545   327 caffe.cpp:259] Optimization Done.

3.11 试改进标准的反向传播算法，提高训练速度，并给出训练提升的加速比（收敛情况下）。

3.12 将习题3.11中你设计的新算法应用到ImageNet数据集上，得到的精度有没有受到影响？影响有多大？请调试你的算法保证精度。