主要有以下两个亮点:
- 提出
$pointwise$ $group$ $convolution$ 来降低$PW$ 卷积(也即是 1*1 卷积)的计算复杂度。 - 提出
$channel$ $shuffle$ 来改善跨特征通道的信息流动。
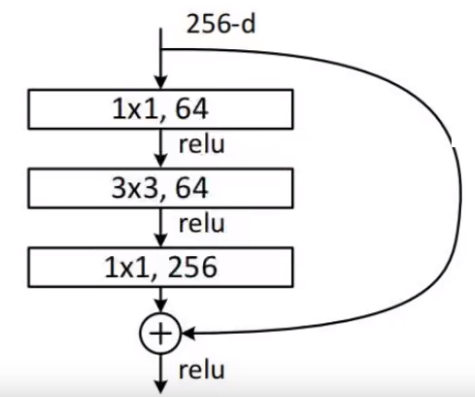
先简单介绍一下
那么为什么
其实是由于
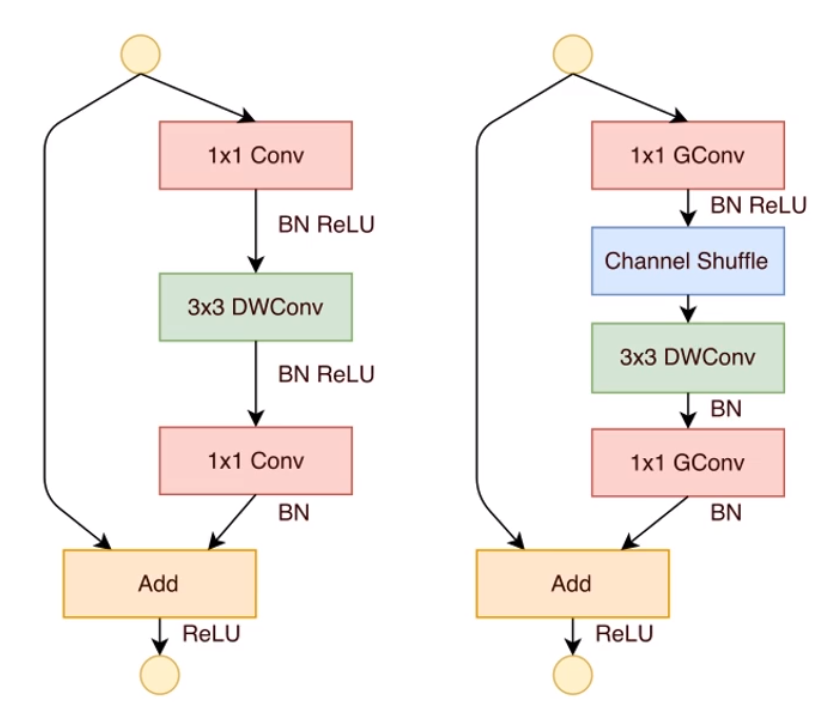
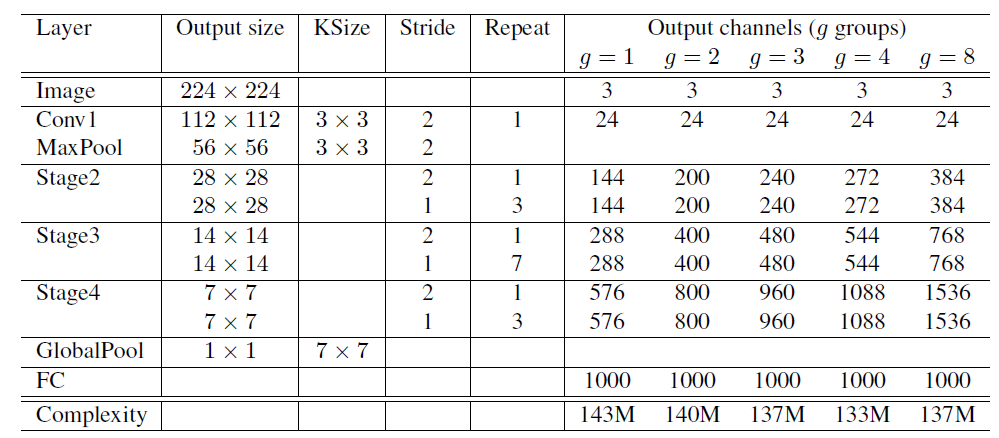
在原论文中作者也给出了
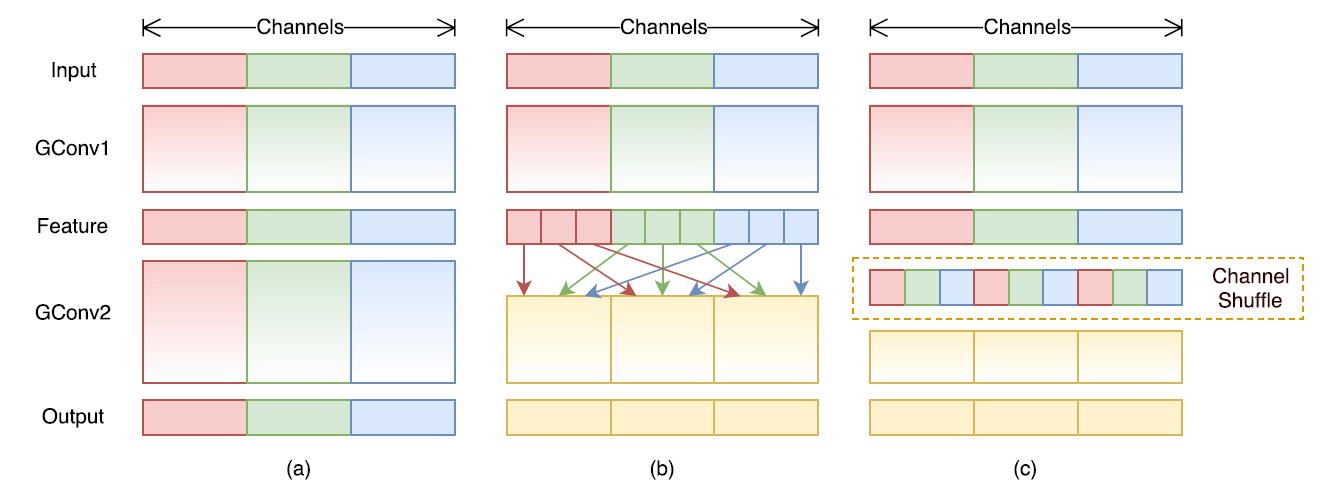
由上可知,虽然
为达到特征之间通信目的,作者提出了
def shuffle_channels(x, groups):
"""shuffle channels of a 4-D Tensor"""
batch_size, channels, height, width = x.size()
assert channels % groups == 0
channels_per_group = channels // groups
# split into groups
x = x.view(batch_size, groups, channels_per_group,
height, width)
# transpose 1, 2 axis
x = x.transpose(1, 2).contiguous()
# reshape into orignal
x = x.view(batch_size, channels, height, width)
return x上图
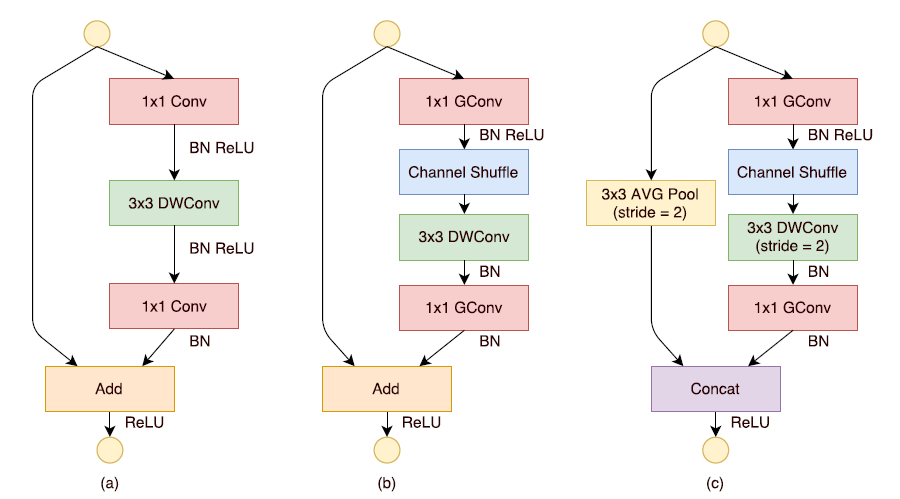
现在,进行如下的改进:将密集的
对于残差单元,如果
# stride$=1
class ShuffleNetUnitA(nn.Module):
"""ShuffleNet unit for stride=1"""
def __init__(self, in_channels, out_channels, groups=3):
super(ShuffleNetUnitA, self).__init__()
assert in_channels == out_channels
assert out_channels % 4 == 0
bottleneck_channels = out_channels // 4
self.groups = groups
self.group_conv1 = nn.Conv2d(in_channels, bottleneck_channels,
1, groups=groups, stride=1)
self.bn2 = nn.BatchNorm2d(bottleneck_channels)
self.depthwise_conv3 = nn.Conv2d(bottleneck_channels,
bottleneck_channels,
3, padding=1, stride=1,
groups=bottleneck_channels)
self.bn4 = nn.BatchNorm2d(bottleneck_channels)
self.group_conv5 = nn.Conv2d(bottleneck_channels, out_channels,
1, stride=1, groups=groups)
self.bn6 = nn.BatchNorm2d(out_channels)
def forward(self, x):
out = self.group_conv1(x)
out = F.relu(self.bn2(out))
out = shuffle_channels(out, groups=self.groups)
out = self.depthwise_conv3(out)
out = self.bn4(out)
out = self.group_conv5(out)
out = self.bn6(out)
out = F.relu(x + out)
return out
# -----------------------------------------------------------
# stride$=1
class ShuffleNetUnitB(nn.Module):
"""ShuffleNet unit for stride=2"""
def __init__(self, in_channels, out_channels, groups=3):
super(ShuffleNetUnitB, self).__init__()
out_channels -= in_channels
assert out_channels % 4 == 0
bottleneck_channels = out_channels // 4
self.groups = groups
self.group_conv1 = nn.Conv2d(in_channels, bottleneck_channels,
1, groups=groups, stride=1)
self.bn2 = nn.BatchNorm2d(bottleneck_channels)
self.depthwise_conv3 = nn.Conv2d(bottleneck_channels,
bottleneck_channels,
3, padding=1, stride=2,
groups=bottleneck_channels)
self.bn4 = nn.BatchNorm2d(bottleneck_channels)
self.group_conv5 = nn.Conv2d(bottleneck_channels, out_channels,
1, stride=1, groups=groups)
self.bn6 = nn.BatchNorm2d(out_channels)
def forward(self, x):
out = self.group_conv1(x)
out = F.relu(self.bn2(out))
out = shuffle_channels(out, groups=self.groups)
out = self.depthwise_conv3(out)
out = self.bn4(out)
out = self.group_conv5(out)
out = self.bn6(out)
x = F.avg_pool2d(x, 3, stride=2, padding=1)
out = F.relu(torch.cat([x, out], dim=1))
return out
后面的
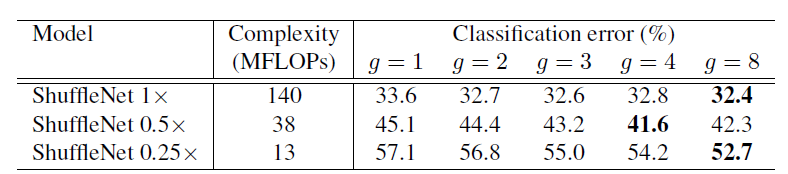
作者做了大量的对比实验来证明
图
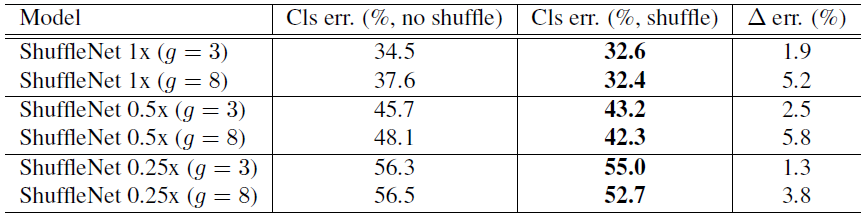
除此之外,作者还对比了不采用
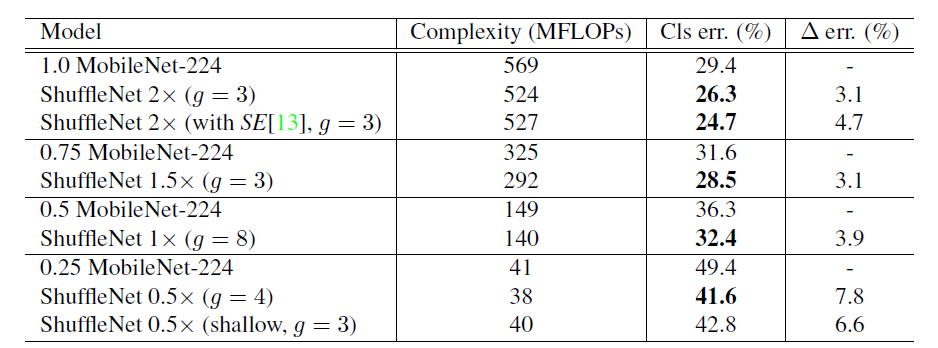
作者也对比了
其他一些实验对比结果大家可以阅读原论文获取。原论文链接放在了引用中,大家自提哈。
- https://arxiv.org/abs/1707.01083
- https://zhuanlan.zhihu.com/p/32304419
- https://www.jianshu.com/p/c5db1f98353f
- https://www.cnblogs.com/hellcat/p/10318630.html
- https://blog.csdn.net/weixin_43624538/article/details/86155936
- https://www.sogou.com/link?url=hedJjaC291MBtMZVirtXo7CqjI0tE6P91nAMx5j2isv6gED9wOCRuw..