主要有以下一些亮点:
- 提出了四个高效网络设计指南
$G1$ 、$G2$、$G3$、$G4$ - 针对
$ShuffleNet$ -$V1$ 的两种$unit$ 做了升级
在
目前衡量模型复杂度的一个通用指标是
是不是准确率和
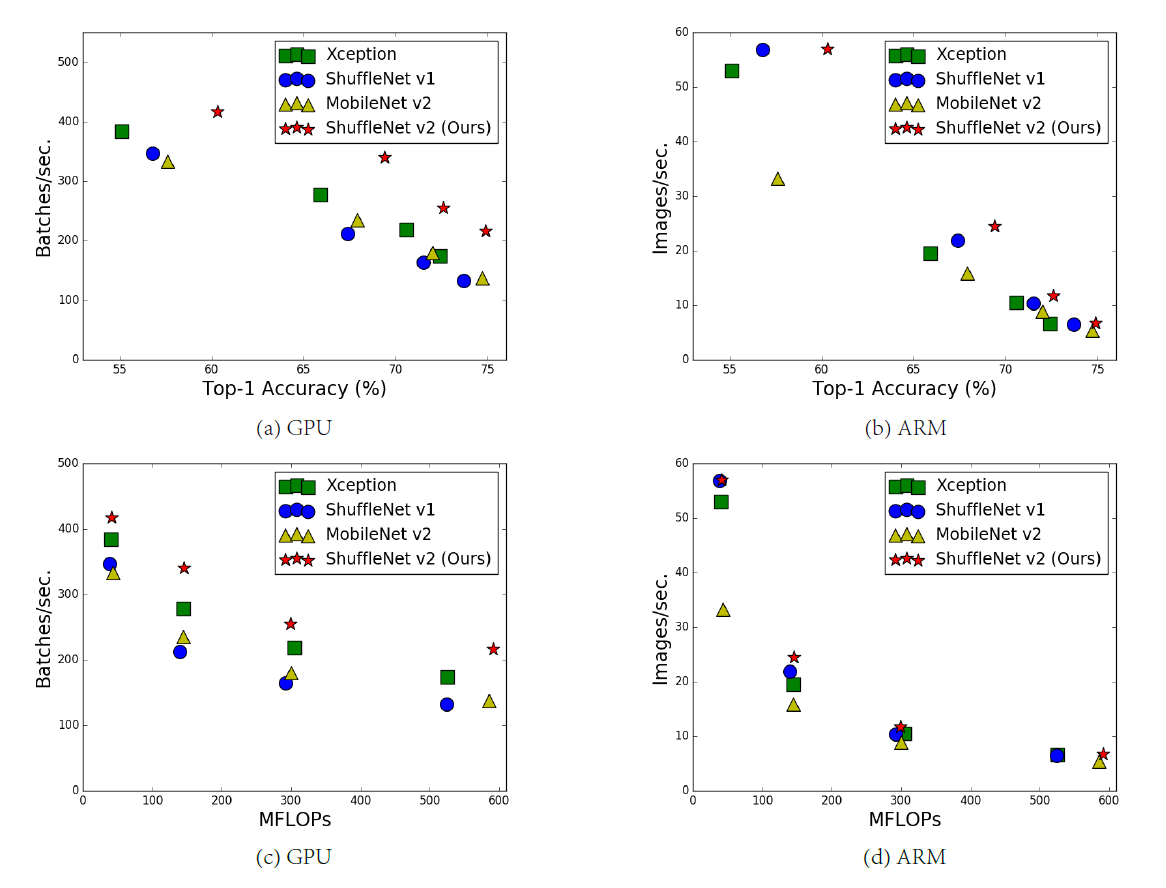
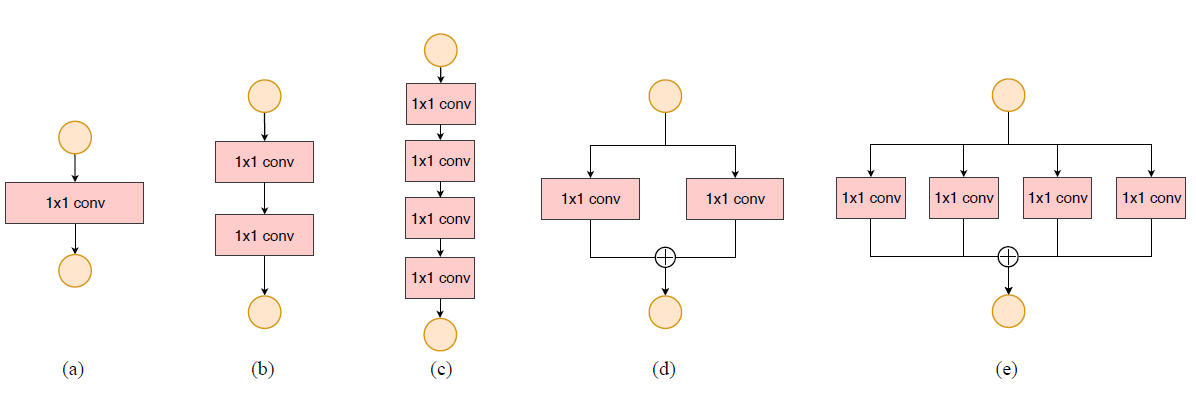
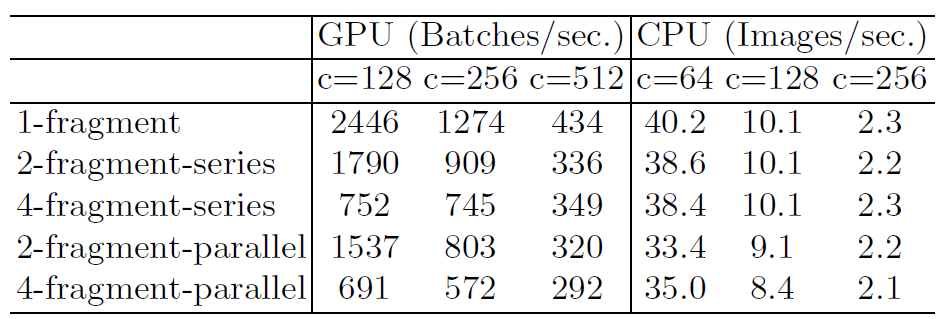
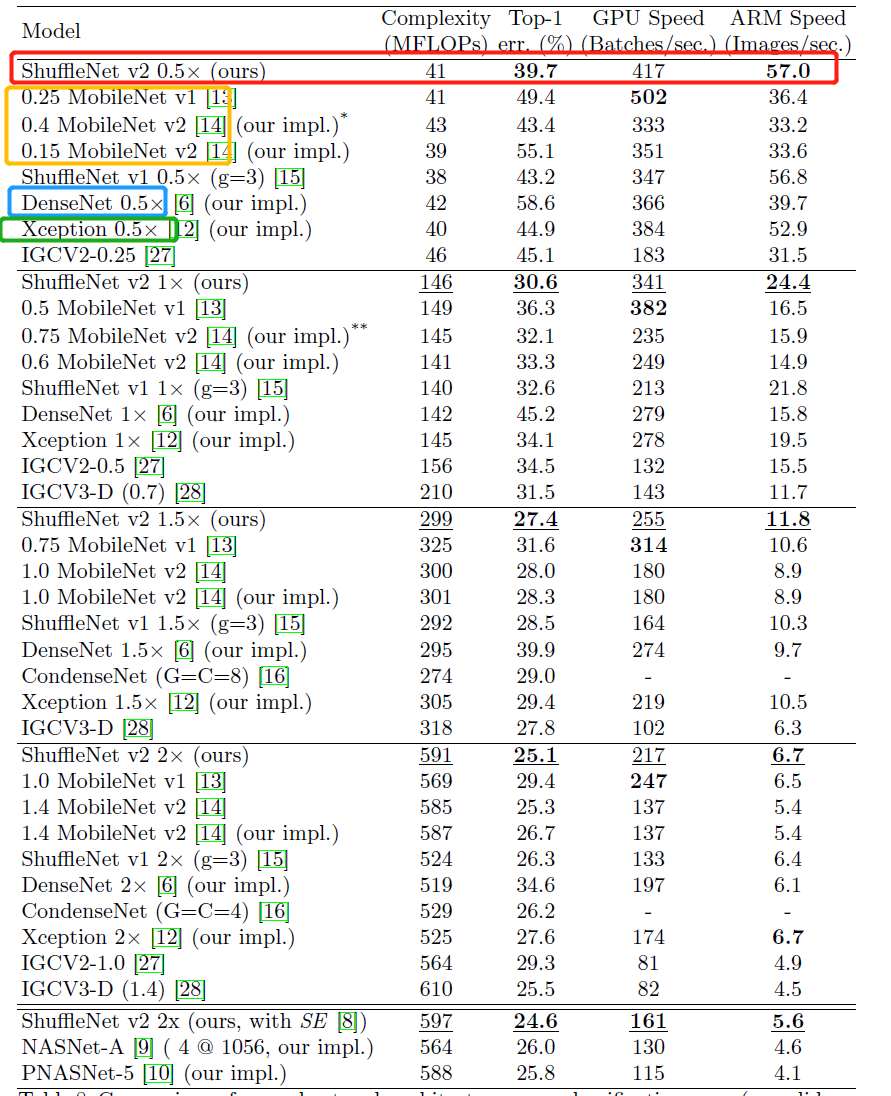
为此他们做了如下的实验:比较了分别以
从图中我们可以看出:
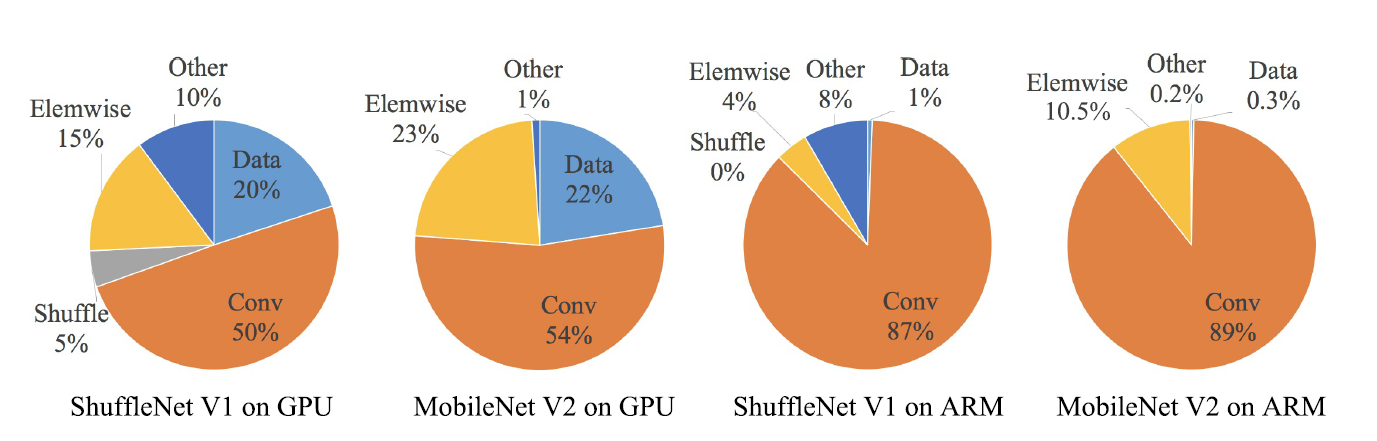
作者经过分析后,认为出现这种情况的原因主要有:
-
对推理速度影响较大的因素,但没有影响到
$FLOPs$ 。例如:内存访问成本$MAC$ ($memory$ $access$ $cost$ )和并行度($degree$ $of$ $parallelism$ )。 -
运行平台不同。不同的运行平台,针对卷积等操作有一定的优化,例如
$cudnn$ 等。
据此作者提出了
(1)使用直接度量方式如速度代替 FLOPs。
(2)在同一环境平台上进行评估。
如下图
综上两个实验,作者提出了四个高效网络设计指南
$$ B=(hwc_111*c_2)=hwc_1c_2 $$
对应的 MAC(
$$ MAC=hwc_1+hwc_2+11c_1*c_2=hw(c_1+c_2)+c_1c_2 $$
并且我们知道以下均值不等式:
最后整理一下上面的式子可以知道:
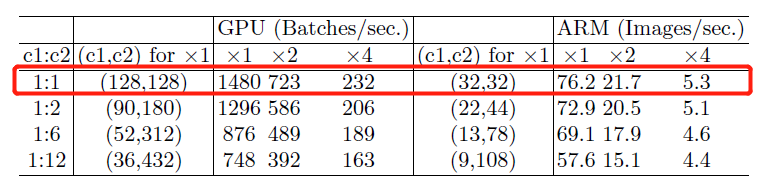
那么在相同
$$ B=hw(c_111*c_2)/g=hwc_1c_2/g $$
其
可以看出,在
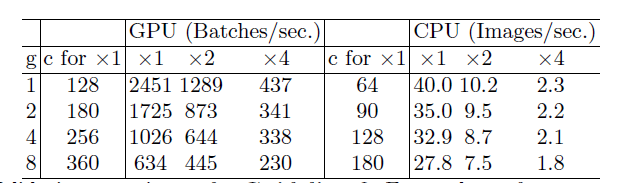
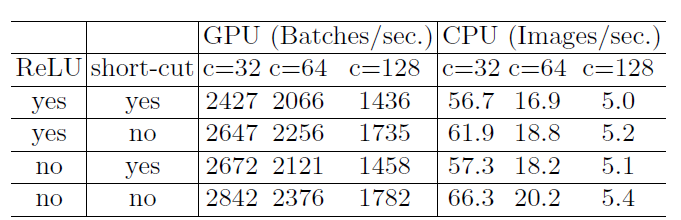
为了研究
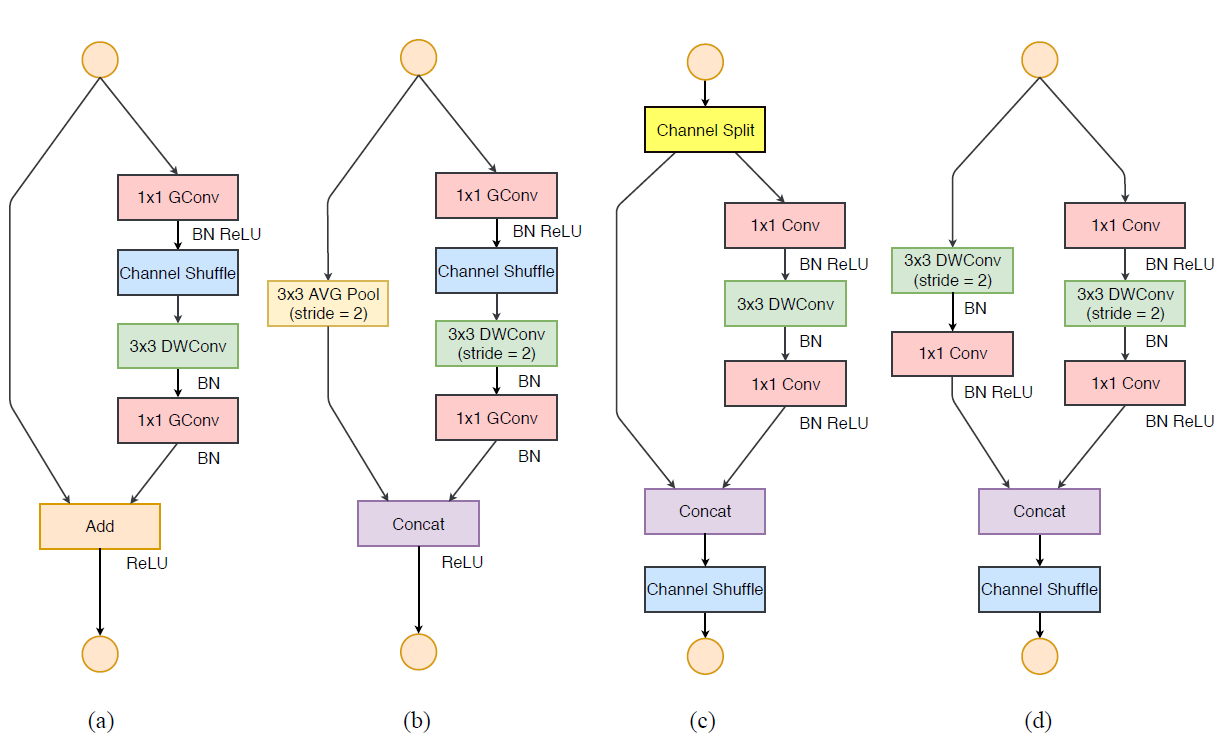
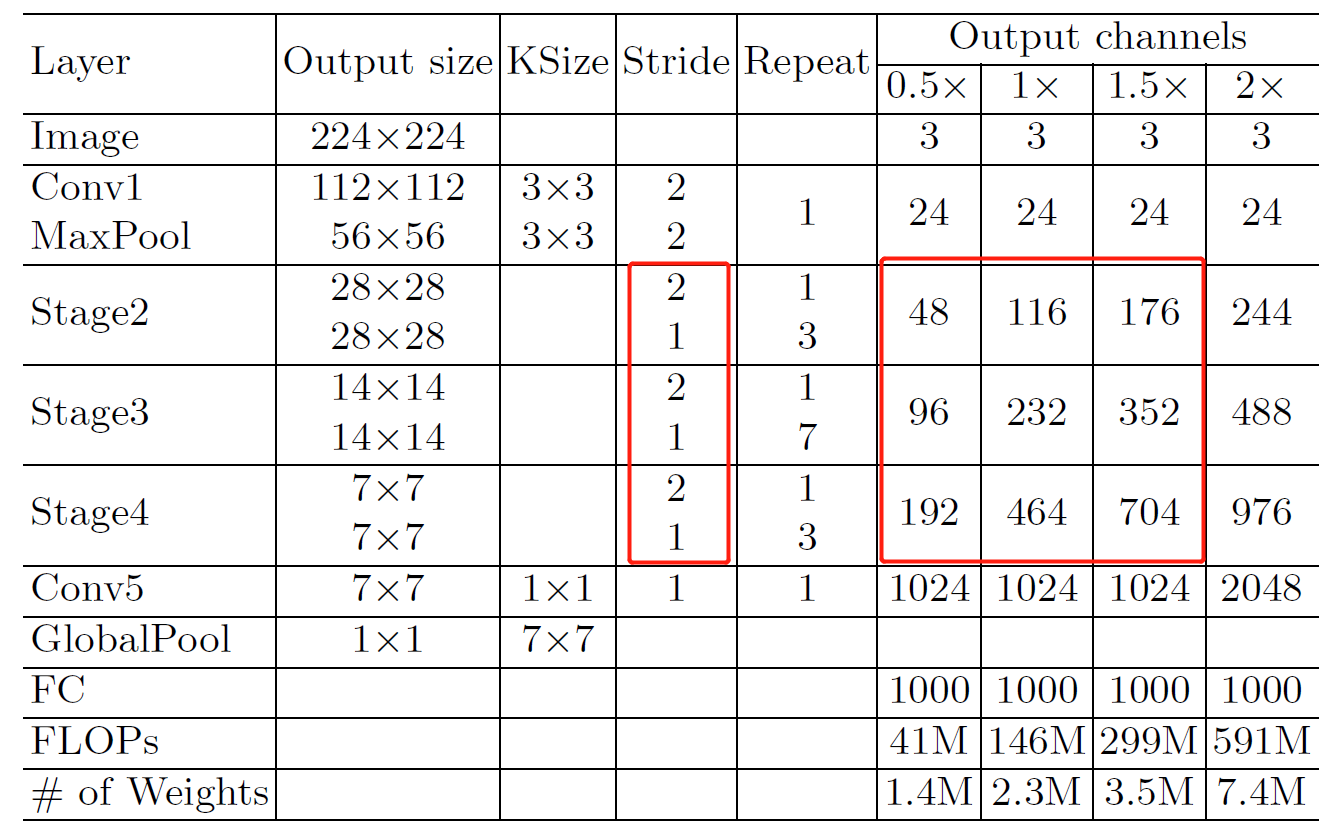
终于到了最后的部分了!这一部分,作者根据之前所提出的设计指南,在
作者在遵循 G1-G4 的设计准则的条件下,对于
作者分析了原
1、图
2、图
3、图
4、图
针对于以上问题,作者在
1、对于
2、卷积之后,把两个分支拼接(
3、对于
如下所示为
def channel_shuffle(x: Tensor, groups: int) -> Tensor:
batch_size, num_channels, height, width = x.size()
channels_per_group = num_channels // groups
# reshape
# [batch_size, num_channels, height, width] -> [batch_size, groups, channels_per_group, height, width]
x = x.view(batch_size, groups, channels_per_group, height, width)
x = torch.transpose(x, 1, 2).contiguous()
# flatten
x = x.view(batch_size, -1, height, width)
return x
class InvertedResidual(nn.Module):
def __init__(self, input_c: int, output_c: int, stride: int):
super(InvertedResidual, self).__init__()
if stride not in [1, 2]:
raise ValueError("illegal stride value.")
self.stride = stride
assert output_c % 2 == 0
branch_features = output_c // 2
# 当stride为1时,input_channel应该是branch_features的两倍
# python中 '<<' 是位运算,可理解为计算×2的快速方法
assert (self.stride != 1) or (input_c == branch_features << 1)
if self.stride == 2:
self.branch1 = nn.Sequential(
self.depthwise_conv(input_c, input_c, kernel_s=3, stride=self.stride, padding=1),
nn.BatchNorm2d(input_c),
nn.Conv2d(input_c, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(branch_features),
nn.ReLU(inplace=True)
)
else:
self.branch1 = nn.Sequential()
self.branch2 = nn.Sequential(
nn.Conv2d(input_c if self.stride > 1 else branch_features, branch_features, kernel_size=1,
stride=1, padding=0, bias=False),
nn.BatchNorm2d(branch_features),
nn.ReLU(inplace=True),
self.depthwise_conv(branch_features, branch_features, kernel_s=3, stride=self.stride, padding=1),
nn.BatchNorm2d(branch_features),
nn.Conv2d(branch_features, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(branch_features),
nn.ReLU(inplace=True)
)
@staticmethod
def depthwise_conv(input_c: int,
output_c: int,
kernel_s: int,
stride: int = 1,
padding: int = 0,
bias: bool = False) -> nn.Conv2d:
return nn.Conv2d(in_channels=input_c, out_channels=output_c, kernel_size=kernel_s,
stride=stride, padding=padding, bias=bias, groups=input_c)
def forward(self, x: Tensor) -> Tensor:
if self.stride == 1:
x1, x2 = x.chunk(2, dim=1)
out = torch.cat((x1, self.branch2(x2)), dim=1)
else:
out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)
out = channel_shuffle(out, 2)
return out如图
1、$ShuffleNet$-$V2$ 完善了网络性能对比的准则,以
2、提出了四个高效网络设计指南,并据此设计了